Amplitude amplification, estimation, Grover, and Quantum walk search

1. Introduction Grover’s algorithm, initially devised to solve unstructured search problems, offers a significant improvement over classical algorithms. While classical algorithms necessitate $\Omega(N)$ queries, Grover’s algorithm accomplishes the task with a mere $O(\sqrt{N})$ queries (grover1996fast). Although the speedup provided by Grover’s algorithm is quadratic, in contrast to the exponential speedup offered by some quantum algorithms solving hidden subgroup problems (such as Shor’s algorithm), it compensates with its broader applicability.Amplitude amplification is the central idea of the Grover, empowering it with quadratic speedup. The primary function of amplitude amplification is to escalate one of the amplitude of a given state decomposition, thereby achieve control over the probability of measurement outcomes. It is one of the most fundamental subroutines in quantum computing and constitutes many other advanced quantum algorithms.Combining Amplitude amplification with QPE, one can estimate the value of the amplitude value of given state, and this is Amplitude estimation. Further combining Amplitude estimation with Quantum walk gives so-called Quantum walk search (i.e. Segedy’s: szegedy2004spectra), which provides quadratic speed-up on the task of searching on a graph comparing to the classical Random walk search.

2. Overview of Amplitude Amplification 2.1. Householder operator Householder operator, also known as reflection operator, is the analogue of Householder transformation in a Hilbert space[1], which is central technique in amplitude amplification. Given a state $|{\psi}\rangle$ with its orthogonal decomposition $|{\psi}\rangle=\sin{\theta}|{\phi_0}\rangle+\cos{\theta}|{\phi_1}\rangle$,
a Householder operator $R_{0}$ reflects $|{\psi}\rangle$ across a hyperplane orthogonal to $|{\phi_0}\rangle$, which corresponds to the Fig 1:
\begin{equation}
R_0=I-2|{\phi_0}\rangle \langle{\phi_0}| \label{aa_householder}
\end{equation}
We will refer to it as “reflection” in the following sections.

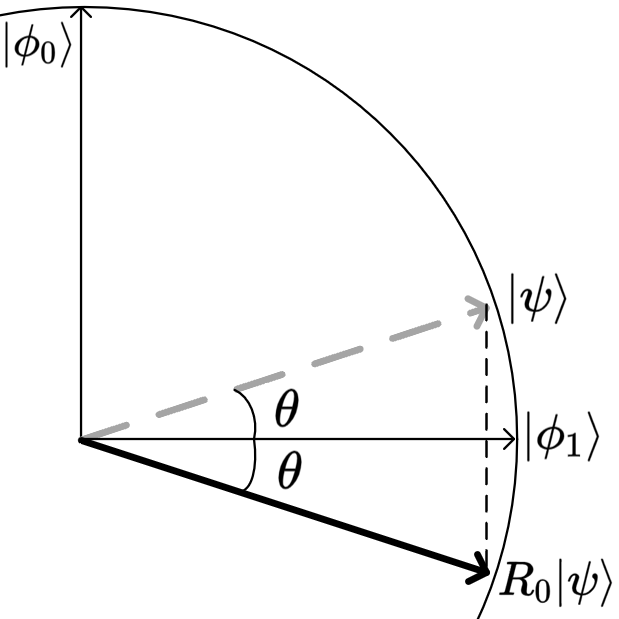
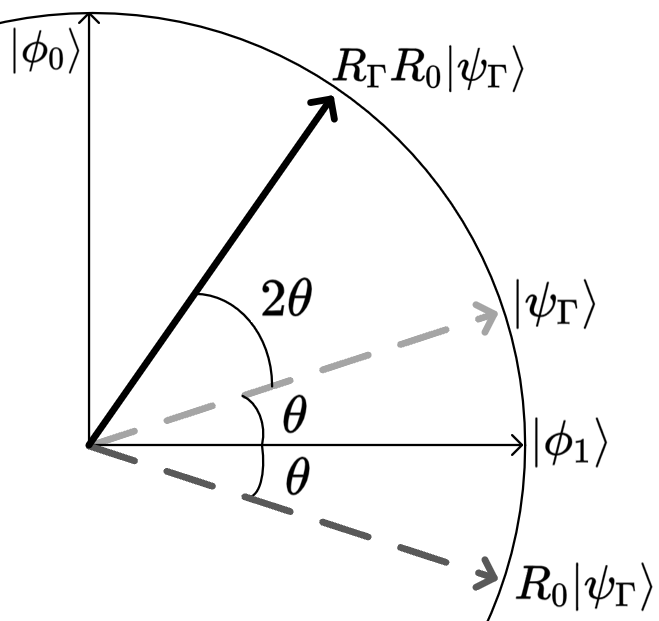
Fig 1&2 : Depictions of the action of the reflection operators

2.2. Binary classification by amplitude amplification Given a set $\Gamma$ of known size that can be binary classified and has a known classification criterion $f:\Gamma\to \{0,1\}$, we want a quantum algorithm that implements the criterion and performs the classification.

In Hilbert space, this problem can be modeled as follow: given a superposition state $|{\psi}\rangle$ encoding the elements of the set, note $|{{\psi}_\Gamma}\rangle$ as a linear combination of two orthogonal basis states encodes respectively two parts of elements according to $f$.
\begin{equation}
|{\psi_\Gamma}\rangle=\sin{\theta}|{\phi_0}\rangle+\cos{\theta}|{\phi_1}\rangle
\label{AA_orthogonal}
\end{equation}

We want to design a quantum circuit to adjust the amplitude of one of the basis states, so that we can measure it out with high probability. For example, if $|{\phi_0}\rangle$ is the desired state, then we want to design a series of unitary operators acting on $|{{\psi}_\Gamma}\rangle$, so that make the amplitude of $|{\phi_0}\rangle$ in the final state approximate to $1$.

The amplitude amplification algorithm achieves this goal by alternating two different reflections. These two reflection operators, denoted as $|{R_\Gamma}\rangle$ and $|{R_0}\rangle$, collectively constitute the amplitude amplification operator $G$:
\begin{equation}
R_\Gamma=I-2\left|\psi_\Gamma\right\rangle \left\langle\psi_\Gamma\right|,
R_0=I-2\left|\varphi_0\right\rangle \left\langle\varphi_0\right|,
G=-R_\Gamma R_0.
\label{aa_operators}
\end{equation}
Applying $R_0$ correspondents to the householder depiction:
\begin{equation}
R_0|{\psi_\Gamma}\rangle=-\sin{\theta}|{\phi_0}\rangle+\cos{\theta}|{\phi_1}\rangle
\label{aa_invariant}
\end{equation}
The action of $G$ on $|{\psi}\rangle$ results in a rotation with a parameter of $2\theta$:
\begin{equation}
G|{\psi_\Gamma}\rangle=\sin{3\theta}|{\phi_0}\rangle+\cos{3\theta}|{\phi_1}\rangle,
\label{aa_rotation}
\end{equation}
\begin{equation}
\left[G\right]_{\mathcal{B}}= \left[\begin{matrix}\cos{\left(2\theta\right)}&-\sin{\left(2\theta\right)}\\\sin{\left(2\theta\right)}&\cos{\left(2\theta\right)}\\\end{matrix}\right],
\label{aa_rotation_representation}
\end{equation}
where the above matrix representation of $G$ is restricted in 2-dimensional space $\mathcal{B}$ spanned by $\{|{\psi_0}\rangle,|{\psi_1}\rangle\}$.
\\\\
Figure 1 gives a geometry interpretation of aa_rotation, where $\ket{\psi_\Gamma}$ got closer to $\ket{\phi_0}$ after applying $G$.

3. Overview of Grover algorithm 3.1. Oracle In classical algorithms, an oracle is a subroutine that operates as a “black box” and is anticipated to return a value based on any input instance of a computational problem. Unlike ordinary subroutines relied by an algorithm, oracles are typically only declared in the algorithm and not yet implemented, which is why they are referred to as “black boxes”.
\\\\
A good example is the predicate function that required by the search algorithm in the C++ Standard Library [1]. For instance, when we want to search even integers in an array, we need to implement a predicate function that will return $true$ when $2$ divides the input element, and will return $flase$ otherwise :
\begin{lstlisting}
bool pred(int i)
{
if (i%2==0) {
return true;
} else {
return flase;
}
}
\end{lstlisting}
\vspace{1em}
In quantum algorithms, the oracle works in a manner that is entirely similar. The difference is that it is a unitary operator and returns a quantum state. The corresponding example is the oracle operator in the Grover algorithm.
\\\\
Given a set $\Gamma=\{x_0,…,x_{N-1}\}$ such that $\abs{\Gamma}=N=2^n$, and a subset $M\subseteq \Gamma$ which contains $m$ elements that have been marked according to a criterion $f:\Gamma \to \{0,1\}$. :
\begin{equation}
f\left(x\right)=\left\{\begin{matrix}
1,x\in M,\\ 0,x\notin M.
\end{matrix}\right.
\label{grover_criterion}
\end{equation}
\\\\
Given a superposition state $\ket{\psi_\Gamma}=\frac{1}{\sqrt{N}}\sum_{i=0}^{N-1}\ket{i}$ \label{grover_def_set} encoded with the labels of $\Gamma$, we want an unitary operator $O_f$ implements $f$ so that it can distinguish a state with the label of marked elements among the superposition state:
\begin{equation}
O_f\ket{i}=(-1)^{f({x_i})}\ket{i}
\label{grover_oracle}
\end{equation}
This is the Grover oracle operator, and it is also a part of the amplitude amplification process in Grover algorithm.

3.2. Unstructured search by Grover Solving an unstructured search problem is almost same solving a binary classification problem: classify a binary-classifiable set $\Gamma$ defined as grover_def_set into a set $M$ that meets the search criterion $f$. The word “unstructured” means that we do not have any other prior knowledge except the above definition.\label{grover_math_prob}
\\\\
Our quantum algorithm needs to amplify the probability of obtaining the target state upon measurement. We will use the previously introduced Grover oracle grover_oracle and amplitude amplification aa_operators technique to achieve this.
\\\\
We start from a uniform superposition state $\ket{\psi_\Gamma}$ that encodes the index of all elements of $\Gamma$:
\begin{equation}
\ket{\psi_\Gamma}=\frac{1}{\sqrt{N}}\sum_{i=0}^{N-1}\ket{i}.
\label{grover_superposition_state}
\end{equation}
The above state can be prepared by applying Hadamard gates:
\begin{equation}
H^{\otimes n}\ket{0^n}=\ket{\psi_\Gamma}.
\label{grvoer_hadamard}
\end{equation}
we note:
\begin{equation}
\ket{\phi_0}=\frac{1}{\sqrt{\abs{M}}}\sum_{i:f(x_i)=1}\ket{i},\ket{\phi_1}=\frac{1}{\sqrt{N-\abs{M}}}\sum_{i:f(x_i)=0}\ket{i}
\label{grover_change_basis}
\end{equation}
and recall AA_orthogonal :
\begin{equation}
\ket{\psi_\Gamma}=\sin{\theta}\ket{\phi_0}+\cos{\theta}\ket{\phi_1},
\label{grover_decomp}
\end{equation}
with $\sin{\theta}=\sqrt{\frac{\abs{M}}{N}}$, $\cos{\theta}=\sqrt{\frac{N-\abs{M}}{N}}$.
\\\\
Now we need an Grover oracle operator $O_f$ that implements $f$ as grover_oracle, which in fact performs a reflection AA_fig:householder as well:
\begin{equation}
O_f=I-\ketbra{\phi_0}{\phi_0}
\label{grover_oracle_householder}
\end{equation}
\noindent
Next we construct another reflection operator with respect to $\ket{\psi_\Gamma}$, which is also called the Grover diffusion operator in Grover’s original paper[1]. Note here for the sack of convenience, an global phase of $-1$ will be applied, which will not affect the final measurement outcome:
\begin{equation}
-R_{\Gamma}=-(I-2\ketbra{\psi_\Gamma}{\psi_\Gamma})=H^{\otimes n}(2\ketbra{0^{\otimes n}}-I)H^{\otimes n}
\label{grover_diffusion}
\end{equation}
Combining the above two operators, we have an amplitude amplification operator $G$:
\begin{equation}
G=-R_{\Gamma}R_{0}=H^{\otimes n}(2\ketbra{0^{\otimes n}}-I)H^{\otimes n}O_f
\label{grover_aa}
\end{equation}
Recall aa_apply_k_times, applying $G$ for $k$ times, the complexity of the algorithm would be:
\begin{equation}
O(k)=O(\frac{1}{\theta})=O(\sqrt{\frac{N}{\abs{M}}})
\label{grover_complexity}
\end{equation}
\noindent
Concerning success probability, let $\sin{((2k^*+1)\theta)}= 1$, we get $k^*=\frac{\pi}{4\theta}-\frac{1}{2}$. Since $k$ is an integer, it holds $\abs{k-k^*\leq \frac{1}{2}}$. Without loss of generality, we assume that $\theta \leq \frac{1}{2}$. The success probability could be bound by:
\begin{equation}
sin^2((2k+1)\theta)=sin^2(2\theta(k-k^*)+\frac{\pi}{2})=cos^2(2\theta(k-k^*))\geq cos^2(\theta)\geq 1-\theta^2\geq\frac{3}{4}
\label{grover_proba_bound}
\end{equation}

3.3. Optimality of Grover’s oracle query complexity The Grover algorithm uses the oracle operator of the discriminant function f with a cost of $\sqrt{N}$ queries, compared to the classical algorithm which requires $\Omega(N)$ queries. This demonstrates the advantage of quantum algorithms. Another famous example that showcases the superiority of quantum algorithms is the Deutsch-Jozsa algorithm for solving the constant/balanced judgment problem, which only requires a single query to the oracle operator. This naturally leads to the question: can the query complexity of Grover’s algorithm be further optimized ? The answer is no. For solving unstructured search problems, the query complexity of Grover’s algorithm is optimal[1]. Here we give a general sketch of the proof via quantum adversary method[1, 1]:
\\\\
For the simplicity we assume that only one element with an index of $p$ is marked for an given input set $\Gamma=\{x_0,…,x_i,…,x_{N-1}\}$, and there is an oracle operator $O_{f_p}$ implements an $f_p$:
\begin{equation}
f_p\left(x_i\right)=\left\{\begin{matrix}
1,i=p,\\ 0,i\neq p.
\end{matrix}\right.
\label{grover_criterion}
\end{equation}
\noindent
Let $\ket{\psi^{0k)}}$ denotes the uniform superposition state that our search algorithm starts from. Let $\ket{p}$ be the marked state, using $O_{f_p}$ as the Grover oracle and after $k$ steps of Grover iteration, denotes the final state (without measurement) as $\ket{\psi^{(k)}}$:
\begin{equation}
\ket{\psi^{(k)}}=\prod_{j=1}^k U_jO_{f_p}\ket{\psi^{(0)}},
\label{grover_opt_evol}
\end{equation}
\noindent
where $U_j$ are some unitary operators.\\\\
Further more, in order to compare, assume we have another evolution starts from the same initial state $\ket{\psi^{(0)}}$:
\begin{equation}
\ket{\phi^{(k)}}=\prod_{j=1}^k U_j\ket{\psi^{(0)}},
\label{grover_opt_bg_evo}
\end{equation}
\noindent
such that $\ket{\phi^{(k)}}$ does not involve any information of the solution $\ket{p}$, and can not solve the search problem.
\\\\
Denote the 2-norm gap between the results of two different evolution:
\begin{equation}
\epsilon=\lVert \ket{\psi^{(k)}}-\ket{\phi^{(i)}}\rVert_2
\label{grover_opt_gap}
\end{equation}
To prove optimality, we need to show that:
\begin{equation}
\frac{1}{2}< \epsilon \leq \sum_{i=1}^k\braket{p}{\phi^{(i)}} \label{grover_opt_neq_all} \end{equation} The left inequality means to ensure a sufficient success probability for our algorithm, while the right inequality is the result of scaling after combining equations grover_oracle_householder and grover_opt_evol. \\\\ Assuming that we need at least $T$ queries. For the right-side inequality, using Cauchy-Schwarz inequality: \begin{equation} \sum_{i=1}^k\braket{p}{\phi^{(i)}}\leq \sqrt{\sum_{i=1}^{T-1}2^2}\sqrt{\sum_{i=1}^{T-1}\braket{p}{\phi^{(i)}}^2}\leq 2\sqrt{T-1}\sqrt{\sum_{i=1}^{T-1}\braket{p}{\phi^{(i)}}^2}\leq \frac{T-1}{\sqrt{N}}, \end{equation} and we get $T=\Omega(\sqrt{N})$ 4. Discussion and further reading for Grover and ampitude amplification Grover’s algorithm solves the problem of unstructured search, with its complexity advantage predicated on the fact that the data set is unstructured: that is, we possess no prior knowledge about the structure of the search space. If one wants to conduct a search on a specific spatial structure (on a graph) while maintaining quantum advantage, the mere use of Grover’s search is not enough. A primary technique involves the integration of the quantum phase estimation algorithm 327, forming the quantum walk search algorithm within the framework of quantum walk. This will be discussed in the subsequent chapter QW_SEARCH. \\\\ The capabilities of the original Grover’s algorithm are limited. Firstly, it can only detect one type of target per run. Secondly, the probability of detection decreases if the actual number of iterations is less than or greater than the optimal number of iterations fig:grover_it. A multi-object version of Grover has been proposed[1] by using partial diffusion operator that rotates the state vector by an angle proportional to the number of target objects. Moreover, a deterministic version of Grover has been proposed to theoretically keep the ideal target probability $100\%$ for any size of database by replacing the phase inversion in the refelction by two phase rotation[1]. Besides, adding ancilla to the multi-controlled-Toffoli gates, deploying multistage design[1], adapting variational learning enhancement[1], have been reported as possible techniques to mitigate Grover run-time error. \\\\ Some works attempted to interpret Grover and amplitude amplification from other perspectives, such as from the viewpoints of QSVT[1] or graphical calculus[1]. \\\\ \label{aa_gr_further}Amplitude amplification and Grover have become the most fundamental subroutines in quantum algorithm research. Advanced quantum search algorithms have been developed by combining Grover with other important quantum computing subroutines and computational models: quantum adiabatic[1] \todo{Ref adiabatic chapter}, quantum walk[1] \todo{Ref QW chapter}, and even hybrid quantum walk/adiabatic[1]. Meanwhile, from the viewpoint of solving math problems, quantum algorithms that use amplitude amplification or Grover as subroutine are often seen in solving linear algebra problems[1, 1, 1], statistics problems[1, 1, 1, 1], hidden subgroup problems[1, 1], combinatorial problems[1, 1, 1, 1] and dynamical system problems[1, 1]. \\\\ Amplitude amplification and Grover’s algorithm both rely on an oracle. Although not providing a specific implementation of the oracle may cause confusion for some beginner, when conducting complexity analysis, using query complexity can more conveniently demonstrate the composition of complexity. Requiring an oracle is not an uncommon phenomenon in quantum algorithms. Many other quantum algorithms are oracular. Early algorithms such as Deutsch-Josza[1], Bernstein-Vazirani[1], and Simon’s algorithm[1] are oracular. For advanced algorithms, an empirical understanding is when an algorithm use amplitude amplification or Grover as its subroutine, it is very likely that it is oracular.

@inproceedings{xie2021efficient,
  title={Efficient Regional Memory Network for Video Object Segmentation},
  author={Xie, Haozhe and Yao, Hongxun and Zhou, Shangchen and Zhang, Shengping and Sun, Wenxiu},
  booktitle={CVPR},
  year={2021}
}